Given an array of integers heights representing the histogram's bar height where the width of each bar is 1, return the area of the largest rectangle in the histogram.
Example 1:
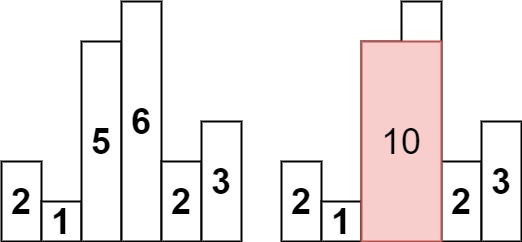
Input: heights = [2,1,5,6,2,3] Output: 10 Explanation: The above is a histogram where width of each bar is 1. The largest rectangle is shown in the red area, which has an area = 10 units.
To solve this problem, we can use a stack to keep track of the heights of the bars in the histogram. We can iterate over the array of heights and, for each bar, we can do the following:
- If the stack is empty or the height of the bar we are currently looking at is greater than the height of the bar at the top of the stack, we push the index of the current bar onto the stack.
- If the height of the bar we are currently looking at is less than the height of the bar at the top of the stack, we keep popping the top of the stack until we either find a bar with a height that is equal to or greater than the current bar, or the stack becomes empty.
At each step, we can calculate the area of the rectangle formed by the current bar and the bars in the stack. The width of the rectangle will be the difference between the current index and the index of the next smallest bar in the stack (or 0 if the stack is empty). The height of the rectangle will be the height of the current bar. We can keep track of the maximum area we have seen so far and return it at the end.
Here is the pseudocode for this algorithm:
function largestRectangleArea(heights):
stack = empty stack
max_area = 0
for i in 0 to heights.length - 1:
while stack is not empty and heights[stack.top()] >= heights[i]:
h = heights[stack.pop()]
w = i - stack.top() - 1
max_area = max(max_area, h * w)
stack.push(i)
while stack is not empty:
h = heights[stack.pop()]
w = heights.length - stack.top() - 1
max_area = max(max_area, h * w)
return max_areaThis algorithm has a time complexity of O(n) since we iterate over the array of heights once and push and pop from the stack at most once for each element in the array. The space complexity is O(n) since we use a stack to store the indices of the bars in the histogram.
The largestRectangleArea function takes in an array of integers heights representing the heights of the bars in a histogram. The function returns an integer representing the area of the largest rectangle in the histogram.
The function first initializes an empty stack and a variable max_area to 0. This max_area variable will keep track of the maximum area of the rectangles we have seen so far.
Next, the function iterates over the array of heights. At each step, it does the following:
- If the stack is not empty and the height of the current bar is greater than or equal to the height of the bar at the top of the stack, it pops the top of the stack.
- At each step, it calculates the area of the rectangle formed by the current bar and the bars in the stack. The width of the rectangle will be the difference between the current index and the index of the next smallest bar in the stack (or 0 if the stack is empty). The height of the rectangle will be the height of the current bar. The function updates
max_areawith the maximum of the currentmax_areaand the area of the rectangle. - After calculating the area of the rectangle, it pushes the index of the current bar onto the stack.
After iterating over the array of heights, the function pops the remaining elements in the stack. For each element popped from the stack, it calculates the area of the rectangle formed by the current bar and the bars in the stack. The width of the rectangle will be the difference between the length of the array of heights and the index of the next smallest bar in the stack (or 0 if the stack is empty). The height of the rectangle will be the height of the current bar. The function updates max_area with the maximum of the current max_area and the area of the rectangle.
Finally, the function returns max_area, which is the area of the largest rectangle in the histogram.


0 Comments